Bonding Curve in Krypto: Erklärung & Funktionsweise Guide

Programme und Plattformen, die auf Blockchains aufgebaut sind, suchen kontinuierlich nach Möglichkeiten, noch dezentraler und automatisierter zu werden. In vielen Protokoll-Ökosystemen sind aktuell immer noch externe Instanzen wie Börsen notwendig, um bestimmte Funktionen auszuführen. Durch den Einsatz von Smart Contracts ist es der Blockchain gelungen, zahlreiche Funktionen stärker zu automatisieren und zu dezentralisieren. Außerdem ermöglicht der vermehrte Einsatz mathematischer Algorithmen eine größere Vielfalt an Transaktionen, die ohne menschliches oder externes Eingreifen ablaufen. Diese Entwicklungen sorgen dafür, dass Blockchain-Protokoll-Ökosysteme immer unabhängiger, dezentraler und automatisierter werden. Ein mathematisches Konzept, das in diesem Bereich zunehmend von sich reden macht, ist der Automated Market Maker (AMM) bekannt als Bonding Curve (Bindungskurve).

Was ist eine Bonding Curve?

Ursprünglich 2017 von Simon de la Rouviere konzipiert, ist eine Bonding Curve ein mathematisches Konzept, das in Plattformen und Anwendungen integriert werden kann, um den Wert eines Tokens auf Basis seines Angebots zu berechnen. Investoren kaufen Token gemäß dem auf der Bonding Curve angegebenen Preis, im Tausch gegen Sicherheiten in Fiatwährungen oder anderen Kryptowährungen wie Bitcoin (BTC) und Ethereum (ETH). Die Wertermittlung des Tokens über die Bonding Curve erfolgt sowohl beim Kauf der Token (wenn sie gemintet werden) als auch beim Verkauf (wenn sie geburnt werden). Während Bonding Curve Token gemintet und geburnt werden, verändert sich das Angebot – was sich wiederum auf den von der Bonding Curve ausgegebenen Wert auswirkt.

Bonding Curves haben mehrere Funktionen:

• Besseres Pricing: Bonding Curves sind transparent, weil sie in Blockchains verankert sind, und gleichzeitig vorhersehbar und präzise, da sie mathematisch definiert werden. Sie bieten einen dynamischeren Ansatz zur Wertberechnung von Kryptowährungen, da sie das Wachstum eines Ökosystems berücksichtigen. Eine Bonding Curve erkennt an, dass mit dem Wachstum des Ökosystems auch die Zahl der entsprechenden Token – und somit auch deren Wert – zunimmt.

• Vorgabe der Wertentwicklung von Token: Eine Bonding Curve legt fest, dass sich der Preis eines Tokens oder Coins in Abhängigkeit vom Angebot verändert – steigend oder fallend – und schafft so ein durchgehendes Token-Modell. Ein Entwickler kann durch Auswahl einer bestimmten Kurvenform steuern, wie stark der Wert eines Tokens abhängig vom Angebot wächst.

• Verzicht auf Börsen: Als vollständig automatisierter Market Maker (AMM) ermöglicht die Bonding Curve nicht nur die Preisbestimmung, sondern auch Transaktionen. Der Algorithmus berechnet den Tokenpreis und zeigt ihn dem Nutzer an, der direkt kaufen oder verkaufen kann. Dies ist ein wesentlicher Fortschritt hin zu noch größerer Dezentralisierung im Kryptobereich.

• Mehrere Token im selben Ökosystem: Durch das Minten eigener Token können Bonding Curves auch mehrere Token innerhalb eines Ökosystems ermöglichen. Ein Entwickler kann verschiedene Bonding Curves implementieren und so mehrere Token für unterschiedliche Anwendungen und Projekte nutzen. Das erhöht die Flexibilität, da verschiedene Token über unterschiedliche Blockchains hinweg eingesetzt werden können – je nach Funktionalität und je nach Verbindung durch Smart Contracts oder Two-Way-Pegs.

Wie funktioniert eine Bonding Curve?

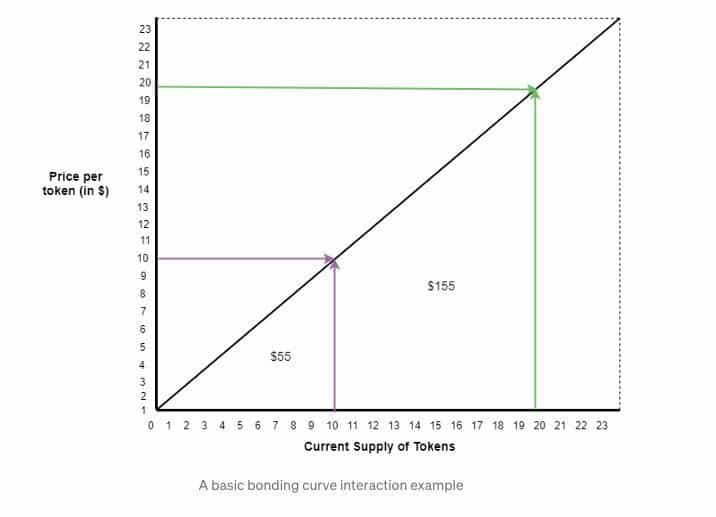
Eine einfache lineare Bonding Curve beschreibt die Beziehung x = y, also Tokenangebot = Tokenwert. Das bedeutet, Token Nummer 10 kostet 10 US-Dollar, Token Nummer 20 kostet 20 US-Dollar. Allerdings zahlt ein Investor, der zehn Token kauft, nicht einfach 10 Dollar. Token 1 kostet 1 USD, Token 2 kostet 2 USD, Token 3 kostet 3 USD, usw. Wer also zehn Token kaufen will, bezahlt 1+2+3+4+5...=55 USD. Kauft jemand zehn Token, obwohl schon zehn verkauft wurden, bekommt er die Token 11 bis 20, also zahlt er 11+12+13+...=155 USD. Das heißt: Mit einer linearen Bonding Curve machen frühe Investoren überproportional höhere Gewinne.

Eine lineare Bonding Curve

Würden diese Investoren wieder verkaufen, hätte der Early Adopter einen deutlich größeren Gewinn.

Der frühe Investor hat 10 Token für 55 USD gekauft. Durch die weitere Investition des zweiten Nutzers steigt der Tokenpreis, womit der Early Adopter zu einem höheren Wert verkaufen könnte.

Sobald der erste Investor seine Token verkauft, werden diese geburnt. Es sind also weniger Token im Umlauf, das Angebot sinkt, und damit auch der Wert. Der zweite Investor, der seine 10 Token für 155 USD gekauft hat, würde jetzt beim Verkauf Verluste erleiden.

Eine Bonding Curve erlaubt es Investoren, jederzeit ein- oder auszusteigen. Allerdings gilt wie bei jeder Investition: Gewinne und Verluste hängen vom Markt ab. Entwickler können bei der Programmierung steuern, wie stark Gewinne oder Verluste der Investoren je nach Einstiegszeitpunkt ausfallen, indem sie die Form der Bonding Curve bestimmen.

Anwendungsfälle von Bonding Curves in Krypto

Bonding Curves wurden erstmals 2017–2018 populär, als Projekte neue Wege zur Kapitalbeschaffung und zum Marktstart suchten. Seither finden sie in diversen Kontexten Anwendung:

Token-Verkäufe und Initial Offerings: Eine Bonding Curve ermöglicht kontinuierliche Tokenverkäufe, im Gegensatz zu klassischen ICOs mit festem Angebot und festem Preis. Frühe Unterstützer kaufen zu niedrigen Preisen, der Preis steigt mit der Nachfrage, sodass die Finanzierung direkt an das Interesse gekoppelt ist. Beispiele sind Fairmints Continuous Organization oder Pump.fun – Letzteres nutzt eine Bonding Curve für Meme-Coins auf Solana, um Liquidität und einen reibungslosen Preisanstieg auch ohne Exchange-Listing zu garantieren.

Automated Market Maker (DEXes): Plattformen wie Uniswap und Curve Finance setzen Bonding Curve-Prinzipien für das Handeln von Tokenpaaren ein. Uniswap nutzt als Kern eine konstante Produktformel (x*y=k) als Bonding Curve, Curve wiederum optimiert Stablecoin-Trading mithilfe einer flachen Kurve für minimale Slippage. Bei diesen DEXs zeigt sich: Mit Bonding Curves lassen sich hohe Liquidität und große Handelsvolumina ohne Zwischenhändler erzielen.

Bonding Curve im Tokenomics-Kontext (Quelle)

Stablecoins (Algorithmisch): Manche algorithmische Stablecoins – wie das gescheiterte TerraUSD – nutzten Bonding Curve-Logik, um das Peg durch steuerbare Angebotsanpassungen aufrechtzuerhalten. Dies ist jedoch risikobehaftet, wie der dramatische UST-Pegverlust zeigte. Andere Projekte wie Ampleforth experimentieren mit ähnlichen Mechanismen zur Preisstabilität.

Governance- und DAO-Token: Auch die Finanzierung von DAOs kann über Bonding Curves stattfinden: Mitglieder zahlen zur Kurve ein und erhalten Governance-Token, deren Preis mit wachsender Beteiligung steigt. Das schafft ein dynamisches Mitgliedermodell; wer geht, verkauft an die Kurve zurück. DAOstack und CommonStack nutzen dieses Prinzip, um Mitgliederbewegungen zu steuern und den Wert für Bestandsmitglieder zu sichern.

NFTs und Digital Art: Im NFT-Segment kommen Bonding Curves zum Einsatz, um den Preis je nach Anzahl verkaufter Ausgaben sukzessive zu erhöhen. Dies belohnt frühe Käufer mit niedrigeren Preisen – wurde aber zum Teil kritisch hinterfragt.

Welche Arten von Bonding Curves gibt es?

Die lineare Bonding Curve ist wohl die einfachste Form – doch je nach Projektziel kann der Entwickler etwa frühe Investments fördern oder frühes Verkaufen erschweren. Die Kurvenform – einmal in die Blockchain integriert und unumkehrbar – legt das Verhalten von Anlegern beim Kauf und Verkauf fest.

Zu den vier beliebtesten Bonding Curves gehören:

1. Sigmoid-Kurve

2. Quadratische Kurve

3. Negative Exponentialkurve

4. Lineare (nicht ansteigende) Kurve

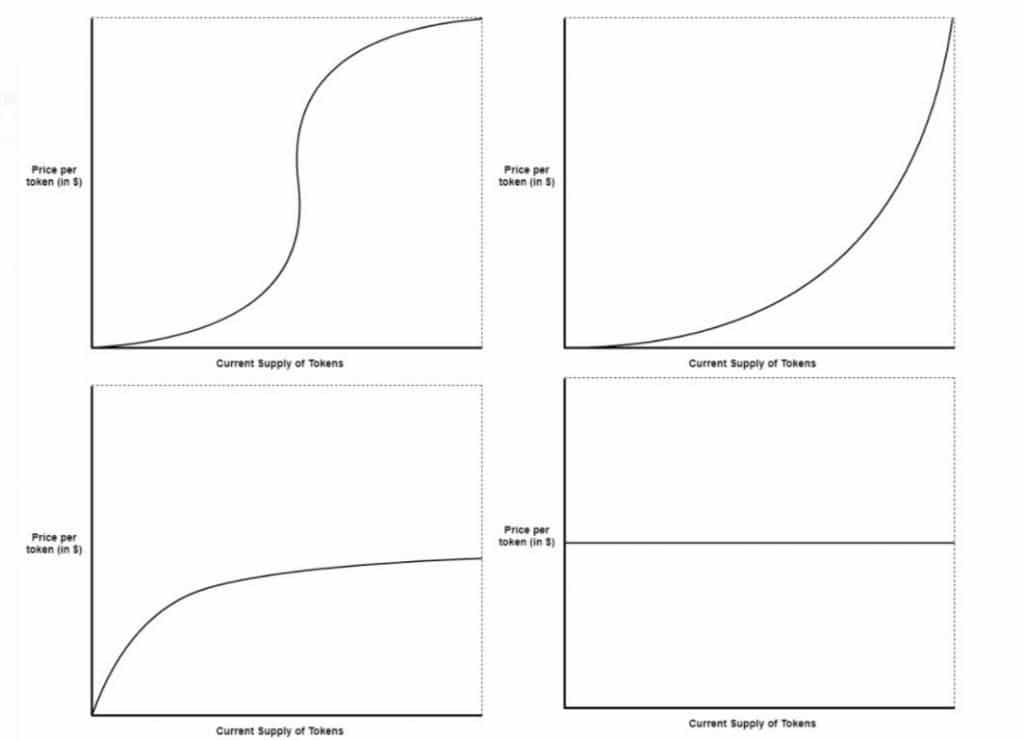
Vier der gängigsten Bonding Curves: Sigmoid (oben links), quadratische Kurve (oben rechts), negative Exponentialkurve (unten links), lineare (nicht ansteigende) Kurve (unten rechts). (Quelle: medium.com)

Je nach gewünschtem Investorenverhalten wird eine bestimmte Kurvenform gewählt (siehe Grafik oben):

• Um frühe Investoren zu belohnen: Wer Early Adopter besonders fördern will, setzt auf Sigmoid- oder quadratische Bonding Curves. Das eignet sich vor allem für Projekte mit Viral-Potenzial, etwa Gaming-Plattformen wie GameFi, NFT-Plattformen wie ECOMI oder Audioplattformen wie Audius. Die Sigmoid-Kurve hält die Kosten für frühe Investoren niedrig und steigt ab einem Wendepunkt rapide an. Die quadratische Kurve steigt gleichmäßiger, bleibt aber für Frühstarter günstiger als für Späteinsteiger.

• Um frühe Investments zu fördern, spätere aber nicht zu benachteiligen: Bei Projekten mit längerer Investitionsphase etwa Fundraisings machen sich negative Exponentialkurven oder lineare Kurven bezahlt. Die negative Exponentialkurve ermöglicht günstige Einstiege zu Projektbeginn, steigt dann aber immer langsamer. Bei linearen Kurven wachsen die Kosten proportional mit der Investorenanzahl; Early Adopter profitieren, doch der Unterschied fällt weniger drastisch aus als bei Sigmoid oder quadratisch.

• Um konstante Kosten zu gewährleisten: Eine lineare (nicht ansteigende) Bonding Curve eignet sich für Projekte ohne Gewinn- oder Verlustabsicht der Investoren. Hier bleibt der Preis konstant; Investoren unterstützen das Projekt aus Überzeugung.

Vorteile von Bonding Curves

1. Stetige Liquidität: Bonding Curves bieten jederzeit einen garantierten Kauf- oder Verkaufspreis direkt aus dem Smart Contract – Marktmacher oder Börsen werden überflüssig.

2. Faires, transparentes Pricing: Die Preisformel ist öffentlich nachvollziehbar und unveränderlich, was Vertrauen schafft und für Chancengleichheit sorgt.

3. Effizientes Fundraising: Projekte können Kapital automatisiert einwerben, der Tokenverkauf passt sich laufend an den realen Bedarf an.

4. Frühzeitige Adoption wird belohnt: Early Adopter erhalten strukturiert günstigere Einstiegspreise, was eine engagierte Community und nachhaltige Projektentwicklung fördert.

5. Automatisiertes Market Making: Im DeFi-Umfeld erleichtern Bonding Curves automatisierte Handelsplätze (AMMs) und demokratisieren das Schaffen von Liquidität.

6. Vorhersehbarkeit für Tokenomics: Projekte können verschiedene Nachfrageszenarien simulieren und dadurch Preisentwicklung und Finanzierung besser planen – für stabilere Tokenomics und weniger spekulative Volatilität.

7. Wertentwicklung an Nutzung koppeln: Bonding Curves können den Token-Wert direkt an die Teilnahme im System binden: Mehr Nutzung führt zu höherem Preis und belohnt die Anwender.

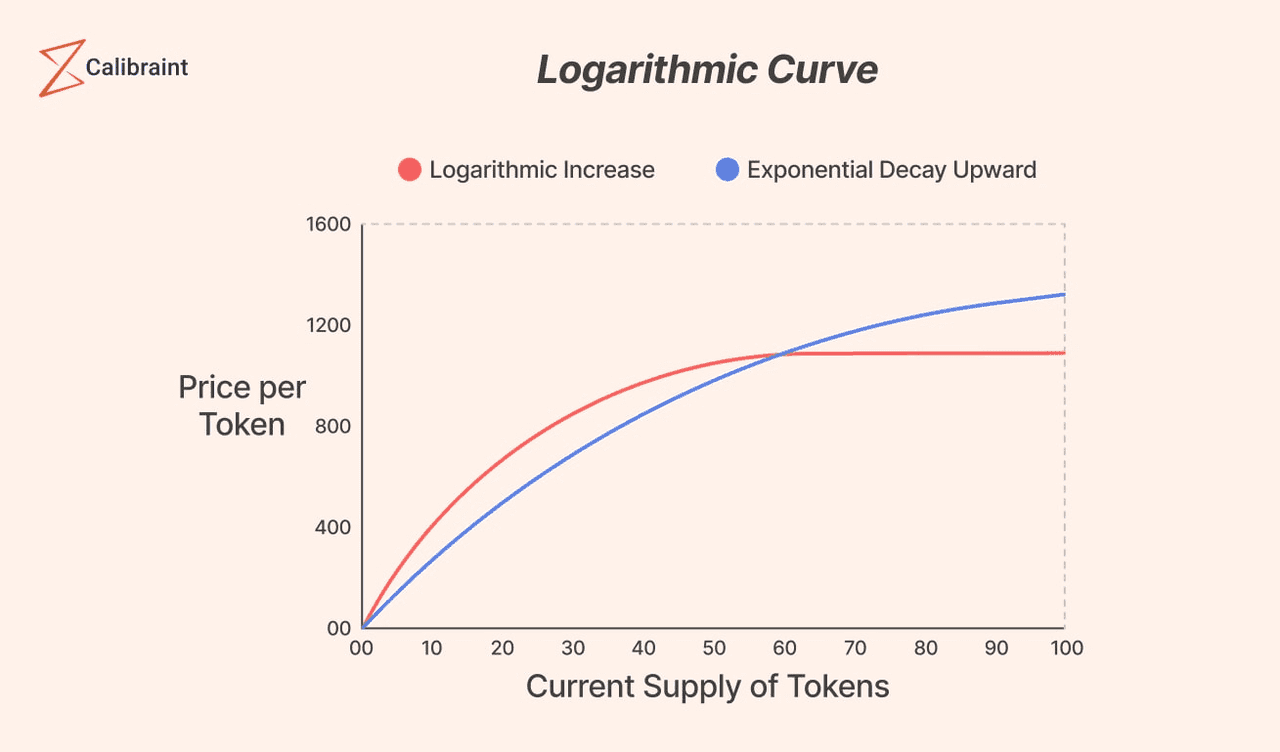
Logarithmische Bonding Curve (Quelle)

Risiken und Herausforderungen von Bonding Curves

Trotz aller Vorteile sind Bonding Curves nicht magisch – sie bringen eigene Risiken und Herausforderungen mit sich:

1. Volatilität & Spekulation: Gerade exponentielle Kurven bergen extreme Preisschwankungen, fördern Spekulation. Frühe Anleger könnten massenhaft verkaufen, was den Preis für Späteinsteiger einbrechen lässt.

2. Whale-Manipulation: Große Käufer oder Verkäufer beeinflussen den Kurs stark: Whales können Kurse aufblasen oder crashen, was Bonding Curves besonders bei kleinen Liquiditätspools anfällig macht.

3. Liquidität vs. Kursauswirkung: Bonding Curves bieten meist gute Liquidität, doch große Einzeltransaktionen verursachen oft Slippage, insbesondere bei steilen Kurven oder kleinen Risiken.

4. Smart-Contract-Risiko: Bonding Curves basieren auf komplexen Smart Contracts, die Sicherheitslücken enthalten können. Fehler ermöglichen eventuell unberechtigtes Minting oder gefährden die Reserveanlagen.

5. Kapitalineffizienz: Manche Modelle binden große Beträge als Liquiditätsreserve – verbunden mit Opportunitätskosten und dem Risiko fehlender Deckung bei falscher Verwaltung.

6. Komplexität & Nutzerverständnis: Bonding Curves sind erklärungsbedürftig, Laien überblicken das Preismechanismus teils nicht, was zu Fehlentscheidungen oder Panikverkäufen führen kann.

7. Risiko von "Bank Runs": Insbesondere bei algorithmischen Stablecoins kann aufgewecktes Misstrauen einen massiven Verkaufsdruck und Kurssturz verursachen, wenn die Reserven schrumpfen.

8. Regulatorische Anforderungen: Bonding Curves können als Wertpapierangebote gewertet werden, insbesondere wenn Spekulationsabsicht vorliegt – eine sorgfältige Rechtsprüfung ist Pflicht.

9. Arbitrage & externe Marktinteraktion: Wenn der Token an anderen Plattformen gehandelt wird, entstehen Preisunterschiede, die Arbitrage-Geschäfte auslösen können.

Fazit

Bonding Curves sind eine spezielle Form des AMM. Über automatisierte, algorithmische Berechnung setzen sie den Tokenpreis entsprechend der gewählten Kurvenform und der vorhandenen Tokenmenge fest. Investoren können Token direkt gegen Sicherheiten kaufen oder verkaufen – alles ohne Zwischenhändler. Das minimiert menschliche Fehler, sorgt für Transparenz, ist automatisiert und dezentralisiert, da alles auf Smart Contracts basiert. Bonding Curves geben Entwicklern die Möglichkeit, ihre Investment-Strategie transparent und fehlerfrei – ganz ohne externe Börsen – umzusetzen. Sie helfen Investoren auch, Kursentwicklungen besser einzuschätzen und potenzielle Gewinne zu kalkulieren. Wichtig: Eine Bonding Curve kann den maximalen Kurs nachzeichnen, garantiert aber nicht, dass die Token tatsächlich gekauft werden – und garantiert somit nicht das Erreichen dieses Werts.

Zusammengefasst sind Bonding Curves ein mächtiges Werkzeug zur Ausrichtung von Anreizen und für flüssige Märkte im Kryptosektor. Sie verkörpern den Geist von DeFi: Die Abschaffung von Mittelsmännern und die direkte Kodierung von Finanzlogik auf der Blockchain. Für Nutzer gilt: Bonding Curves sind das Zusammenspiel von Angebot und Nachfrage auf algorithmischer Basis. Wer an einem Token Sale oder einem DeFi-Protokoll mit Bonding Curves teilnimmt, sollte deren konkrete Ausgestaltung und Auswirkungen verstehen, um informierte Entscheidungen zu treffen.