Many crypto investors are looking to maximize returns while minimizing the overall investment risk. Given the volatility of the cryptocurrency market, reducing the risk is not an easy job. However, there are methods in the investment finance toolbox that can help manage such a risk. One of the most powerful among these tools is the Modern Portfolio Theory (MPT).
What Is Modern Portfolio Theory (MPT)?
MPT is an investment portfolio design methodology seeking to minimize risk for a given expected return on investment (ROI). MPT was introduced in the early 1950s by economist Harry Markowitz, who was later awarded the Nobel Prize in Economics for the development of this theory.
Using MPT, an investor can derive an optimal portfolio of assets that minimizes the investment risk for a specific expected return.
MPT uses the concept of portfolio diversification via correlation analysis to minimize risk. Instead of relying on one asset, an investor can diversify their portfolio with assets that share low or negative correlations, and minimize the overall risk.
The two main assumptions of MPT are that:
- Investors are inherently risk-averse and are looking to minimize their risks
- Assets with low or negative correlations are optimal for risk minimization
MPT has been hailed as a theory with great applicability to the needs of many ordinary people who want to invest without worrying about managing potentially risky portfolios. Many of these investors are not looking for high risk, high return strategies used by some professional traders. Instead, their key goal is risk minimization while still achieving healthy returns.
How to Calculate Portfolio Return and Risk Values in Modern Portfolio Theory?
The process of applying MPT starts with selecting a set of potential assets to evaluate. The more assets included, the more complex the analysis calculations will be. However, most investors or analysts using MPT do not use manual calculations, and instead rely on software. The software can handle any realistic number of assets to be evaluated.
Most software tools used for MPT are custom-written using Excel/VBA, statistical computing packages such as MATLAB and SAS, or programming languages such as R, Python, or C++. There are also some specialized software packages or utilities specifically created for MPT, e.g., the packages from Efficient Solutions and Portfolio Visualizer. In some of these tools, MPT is referred to as the Mean Variance Optimization analysis.
Although software can handle a very large number of assets, it is still advisable to keep the asset numbers to manageable levels. Avoid pouring dozens of potential assets into the simulation software, hoping that the software will spit out the optimal portfolio out of all that variety. It is always best to carefully pre-select a set of assets to evaluate, and then run them through the MPT analysis.
It is also helpful to understand the basic calculation steps behind MPT. Given the scarcity of MPT-specific software, understanding the formulas can help Excel-savvy users to create an MPT tool of their own.

1 Calculate The Expected Return
The first step is to calculate the expected return on each asset individually. Each asset’s expected return is usually based on historical data analysis, past periods’ return figures, technical analysis, and fundamental analysis.
The total portfolio-wide expected return is a weighted average of all the included assets’ returns. Let’s assume for simplicity purposes that we evaluate just two assets, and they have expected return figures of 3% and 5%. Let’s also assume that our simulated portfolio will have 70% of the total funds invested in the first asset, and 30% allocated to the second asset.
Under this scenario, the total portfolio return is:
(3% * 70%) + (5% * 30%) = 3.6%
2 Calculate Estimated Risk Level
After we have our expected return for this portfolio composition, we need the second important figure used in MPT – the estimated risk level for the portfolio.
MPT defines investment risk as the variability of an asset or portfolio. The more variable assets or portfolios are, the more risk is involved.
Assuming our simplified example with two assets, the portfolio risk in MPT is calculated using the following formula:
W1² * STD1² + W2² * STD2² + 2*W1*W2*COV(1,2)
where:
W1 is the weight/share of the first asset in the portfolio, which is 70% in our example,
W2 is the weight/share of the second asset, which is 30% in our example,
STD1 and STD2 are the standard deviations of each of the two assets respectively,
COV(1,2) is the covariance value for the two assets.
If you want to conduct MPT analysis for simple scenarios yourself, the MS Excel software package has all the required formulas. The standard deviation in Excel can be calculated using the STDEV() function, while the covariance between two sets of numbers is calculated using the COVARIANCE.S() function.
However, do note that as the number of assets increases, the formula above gets exponentially more complex. For example, with just four assets, the risk formula will need four standard deviation values, one for each asset, and six covariance values, one for each of the two-asset combinations.
What Is the Efficient Frontier Graph in Modern Portfolio Theory?
As we simulate the risk vs return values by varying portfolio asset weights, we can identify the lowest risk portfolio for each given expected return level.
We can then construct a line graph where the y-axis denotes the expected return levels for the various portfolio combinations, and the x-axis denotes the corresponding lowest-risk values for each return level. This graph, or rather the line on it, is known as the Efficient Frontier.
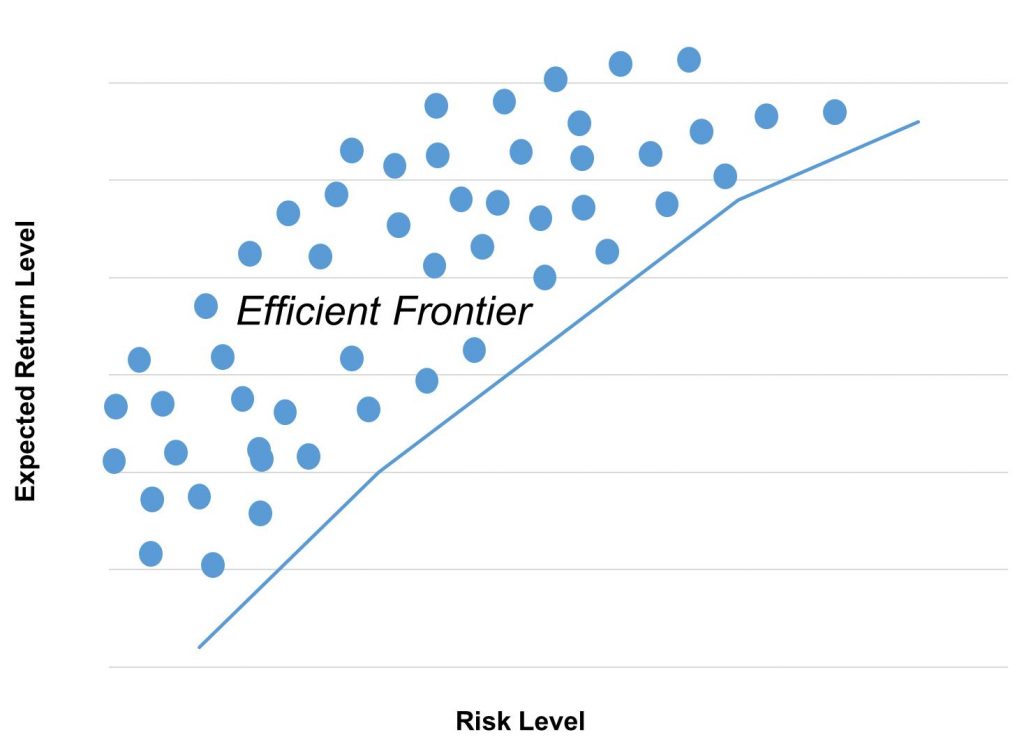
Portfolios that lie on the Efficient Frontier line or above it are the best candidates for investment.
How Does Modern Portfolio Theory Identify the Optimal Portfolios?
Based on the Modern Portfolio Theory formulas, assets with very low and strong negative correlations are usually identified as the best investment options. This is based on the theory of asset diversification. The less correlated (or negatively correlated) assets reduce the overall variability, and thus, the risk in investing.
The central idea is that, during a market downturn, when one class of assets underperforms, the assets uncorrelated or negatively correlated with it are likely to perform much better and balance out the total portfolio performance.
It should also be noted that, under MPT, increasing the number of assets in a portfolio is likely to reduce the risk. However, there is always a trade-off between diversifying into more assets to reduce the risk, and keeping the number of assets in a portfolio manageable.
This point is particularly relevant for individual casual investors who may not be using investment fund portfolio managers with access to tools for analyzing a large number of portfolio items simultaneously.

What Are the Advantages and Disadvantages of Modern Portfolio Theory?
Modern Portfolio Theory has been regarded as a breakthrough theory in investment analysis. Its key advantages are:
- MPT takes into account the needs of risk-averse investors. Many individual investors who are not professional traders would like to devise optimal return portfolios while minimizing risk. They are less likely to follow high-risk strategies employed by some of the professional trading folk. MPT is ideal for these individual investors.
- MPT indirectly forces the investor to diversify their portfolios, a strategy that is often recommended in general to investors under most market scenarios. Thanks to using MPT, investors who would not otherwise entertain the idea of diversifying come to understand the merits of a diverse portfolio.
However, along with its key advantages, Modern Portfolio Theory has some limitations and criticism levied at it:
- One criticism of MPT is that its key measure of risk, portfolio variance, can mask different market scenarios under it. Two portfolios can have the same variance, but the first one might be due to frequent low-degree variability in the assets, while the second one could be due to one or two very sharp changes in the asset prices. The former scenario is not a cause for concern, while the latter points to assets in the portfolio with a potential for wild/risky market swings.
- MPT does not take into account transaction fees associated with trading. Portfolios are evaluated solely on the basis of the expected return and risk. However, trading fees can erode expected returns significantly, particularly in the case of smaller investments.
- MPT’s key formulas assume equal risk regardless of the investment amount. However, investment risks can be substantially different depending on the amounts involved.
In general, despite some of the criticism, MPT has stood the test of time well and has been a valuable tool for risk-averse investors for around seven decades.
Is Modern Portfolio Theory Applicable to Cryptocurrency Investing?
MPT is a universal investment analysis tool and has a lot of merit for crypto investors. MPT favors diversified and uncorrelated portfolio development. The leading crypto assets, Bitcoin (BTC), Ethereum (ETH), and other high-cap cryptos, have recently had low correlations with the traditional stock market and the commodity market.
This makes a combination of crypto assets and traditional stocks a good candidate for evaluation using MPT.
Additionally, some individuals prefer to invest in a mix of different cryptocurrencies. MPT can be used by them to identify optimal crypto investment portfolios. For instance, Bitcoin has had low correlations with some of the top altcoins, and a predominantly BTC-based portfolio diversified with these coins can be a good risk reduction strategy.
The table below shows the correlations of BTC to a number of the leading assets or indices from the stock market, commodities market, and crypto market. A correlation coefficient closer to 1 indicates a strong correlation, a coefficient closer to 0 indicates a weak correlation, and negative values indicate inverse relationships between BTC and the corresponding asset. Typically, correlations above 0.8 are considered strong.
| The correlation to BTC | Jan 1st to Sep 30th, 2021 |
|---|---|
| Grayscale GBTC | 0.89 |
| S&P500 | -0.06 |
| Dow Jones | 0.05 |
| Gold | -0.59 |
| Oil | -0.12 |
| Nasdaq Composite | -0.12 |
| Nasdaq 100 | -0.15 |
| ETH | 0.28 |
| BNB | 0.51 |
| ADA | 0.25 |
| SOL | 0.11 |
The results for the first 9 months of 2021 indicate that BTC is only highly correlated with the Grayscale GBTC crypto index fund. Thus, there is an opportunity for BTC holders to use MPT and investigate potential diversification with the other asset classes or other cryptos.
Conclusion
Modern Portfolio Theory is an investment risk minimization approach that takes into account the needs of risk-averse investors. For each expected return level, it derives an optimal portfolio that minimizes risk.
The assets that minimize risk in MPT typically share low or negative correlations. Diversification via investment in assets with low and negative correlations is at the heart of MPT.
Despite some criticism, MPT has been an effective and valuable tool in the investment toolbox for around seven decades. Although markets and market conditions have changed tremendously over these decades, MPT still has value. Risk-conscious investors, including those in the cryptocurrency market, may use MPT as a valuable tool for diversification and portfolio optimization.
Read More
- What is The Efficient Frontier: Key to Profitable Investing
- Crypto Portfolio Allocation: Should Crypto be Part of Your Portfolio?
- How to Use Risk Parity in Crypto Trading
- Efficient Market Hypothesis (EMH): Does Crypto Follow?
- Crypto Index Funds: Gateway to Low-Risk Cryptocurrency Investing
- What Is Correlation Coefficient: The Essential Diversification Tool
- What is Asset Correlation: A Powerful Weapon for Portfolio Diversification
- How To Do Crypto Research: The Best Ways to Get Started










